Particle
Mass Ratios, and Similar Geometric Volume Ratios
by Carl R. Littmann, added to website in 2000; later revisions where indicated
Whether by coincidence or not, certain particle mass ratios, in physics, are nearly equal to certain geometric ratios in simple patterns. These patterns are somewhat analogous to ‘close packing’ of spheres. This article correlates some of these particle mass ratios with some volumetric ratios in simple patterns. See below, (Stroking frames may show patterns faster)
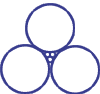
DESCRIPTION: (spheres in drawings below intended perfectly round and touching)
Geometric Pattern (Centers of all spheres coplanar) |
(See Pattern) |
(Important . .Particles) |
ave. Mass Ratio |
|||||||||
|
1 large sphere to 1 small sphere (centered in the pattern): 270.10/1 |
pion+ or pion- to electron: 273.13/1, piono to electron: 264.14/1 |
270.13/1 |
|||||||||
|
3 large spheres to 3 small spheres (all 3 smaller spheres also same size) |
Kaonso or
KaonLo to electron: 973.92/1 |
969.98/1 |
|||||||||
Close Up Views
|
3R13/6r3 + 3R23/6r3 = 1836.00/1, i.e. |
Proton (or antiproton) to electron: 1836.15/1 |
1837.42/1 |
Note, Table I, above, informally shows relationships in an earlier article by me and published in the Journal of Chemical Information and Computer Sciences, 1995, 35, pp. 579-580.
To view two other drawings, each generating a sphere Volume Ratio nearly equal to the 'Proton to electron Mass Ratio', click: ‘case BB-CC' and 'case BBB-CCC'. (More information on them later-on.)
Interestingly, at least 3 Nobel Laureates, all familiar with 'Quark theory', bemoaned not understanding why the various particles in physics have the particular masses they have. And I hope my presentations largely rectify that.
ADDENDUM (2009-2021) – Important:
Over the years, many other basic volume Ratios in sphere patterns have been found that nearly equal the mass Ratios of important particles (relative to the electron mass). These are presented in a newer, more orderly way at http://www.causeeffect.org/articles/book.html
And after glancing at the 'Muon Case', Table II, below, readers should likely 'click' that above link. If, however, the readers opts to continue scrolling-on, to the many topics below, they will still find the basic particles covered well. But for covering the 'D' and 'B' mesons, click the above link.
----------------------------------------------------------------------------------
TABLE II; a Muon Mass Estimate,
Imagine the possibilities when 2 Protons, each with radius 'R',
imagined below, contain medium-size spheres, with radii, r1, r2,
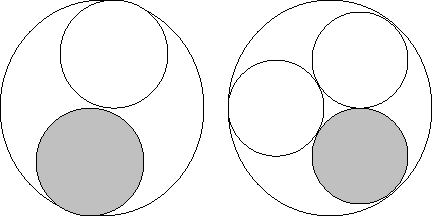
. . . . . . . . . . Case ‘D’ . . . . . . . . . and . . . . . . . . . . Case ‘E’ . . . . . . . . . . .
_____ r1 / R = 0.5/1.0 ____________ r2 / R = 0.46410/1___
Volumetric Ratios: (let us assume the volume of each above large spheres is 1836.15 units).
That corresponds to the actual proton mass equaling 1836.15 ‘electron masses’, (‘me’).
Next, we calculate the average 'volume' of the -shaded- spheres in terms of electron 'masses':
Est. = 1836.15 [ (r1)3 + (r2)3 ] / 2 (R3) = 206.54me est. for muon, using 1836.15 me for ref. proton.
Empirical Muon– (or Antimuon+) mass: 206.77me, and empirical proton mass is 1836.15 me.Thus our above method of estimating the muon mass came out very close.
_____________________________________________________________
Interestingly, there are no compact (standard) particles in the range of "greater than 1 electron mass but less than 200." That is likely because even if such small compact mass tried to spin near the velocity of light, it still could not achieve as much angular momentum as something called, "a Planck's Bar Constant" amount, which relates to "Heisenberg's Uncertainty Principle." But the 'free' electron, outside a nucleus, is not a compact particle. Instead, it is spread-out like a puffball or doughnut. Thus the electron can more easily develop the sufficient angular momentum to exist, and does. _____________________________________________________________
_____________________________________________________________
Now, we present, below, a ‘List of major HYPERON particles’ (very prominent particles and with longer half-lives than most other particles); and along with it – a few other items are presented. Everything on the list is provided with a clickable link to a sphere pattern drawing that predicts each Hyperon mass. (Generally, Hyperon particles and their associated ‘families’ are more complicated than structures in Table I, so some drawing estimates may predict mass outcomes somewhat less precisely, in some cases. More on that later.) Note, where the old term, 'Hyperon' is used below, the newer term, 'Baryon' is preferred.)
Additional supportive drawings may be found by clicking my heading, ‘Booklet of large & small Spheres ..... etc.’, on my Homepage; but the below provides a good introductory foundation:
The Lambda Hyperon particle (Λ0) – click the ‘blue’ at left for a helpful drawing. (Note, the several ways of estimating its mass there, but all lead to the same mass ratio.)
The heaviest and longest life Sigma Hyperon particle. (Σ−), (Again, click the ‘blue’ at left for helpful drawing for this particle.)
The Sigma Hyperon Resonance Energy Σ*+) and associated mass. (Some particles involve themselves more often in special behaviors if enough energy is added to them to raise their energies to a unique energy value, say, E*. So we say, here, that an equivalent mass, m*, is associated with that E*, if m* = E*/c2.)
The lightest and longest life Xi Hyperon particle. Click Link: Smallest mass Xi Hyperon (Ξ0), which covers that particle, and then return to this above Article, and continue.
The heaviest and rather long life Xi Hyperon particle. (Ξ−), (Also, click next line for more details)
The Xi Hyperon Resonance Energy. (Ξ*0)
The Omega Hyperon particle, (Ω−): Click Link: Other Ways to Estimate the Omega Baryon (Ω−) mass, which covers that particle, and then return to this above Article, and continue.
The Higgs Particle. ((Update: In 2017, the physics super-collider particle experts refined their empirical estimates for the mass of the Higgs Boson, still more, and their newest estimate is equivalent to about 133.32 to 133.50 proton masses. That remains gratifyingly close to my platonic-constructed pattern estimate, 133.65 protons. I.e., a major geometry ratio: 133.65 / 1. It seems that nature has an escalating difficulty constructing even very short-life particles of very high masses, like the Higgs Boson. Many competitive factors in nature may also be involved, and cause the actual particle mass values to deviate slightly away from that of the simple geometry ratios shown in my linked drawing.))
Update: A more recently discovered Particle is the Xi Double Charm Baryon, (Greek symbol Ξcc++). ((Its mass is very large, equivalent to 7086.1 electron masses, or almost 4 protons. (But that is still much lighter than the Higgs Boson. That Xi particle was discovered by the super-collider group in 2017.) My drawing shows how it is near the average mass of a pair of already known mass particles. And near the average mass of another pair of already known mass particles -- related to the pair just mentioned. And I have previously often shown that the more pairs of particles, that when averaged together – give an almost identical mass value; the greater chance of finding a real particle in Nature close to that mass. And the likely longer its half-life.))
End of above “List of Major Hyperon particles," and Updates on “Recently discovered other Particles.”
______________________________________________
Important comments about the Tauon Particle, the Eta Prime particle, and the Eta particle:
An interesting relationship seems to exist between the Tauon, Eta Prime, and Eta particles; although the Tauon has an even heavier mass than the Hyperons: If the empirical Tauon (3477.19 equiv. electron masses) is averaged with the average Pion particle (270.10 electrons), a mass of 1873.5 electrons is obtained. That is extremely near the empirical mass of the Eta Prime particle, 1874.1 electrons!
And if that Eta Prime mass (1874.1 electrons) is also averaged with the average Pion particle (270.10 electrons), a mass of 1072.1 electrons is obtained. That seems as close to the empirical mass of the Eta particle, 1072.1 electrons, as one can get!! ____________________________________________
Other Miscellaneous Illustrations and remarks about the most prominent particles:
As one likely noted from the above; just as “Many roads lead to Rome”; also, “Often, several different geometric roads (or patterns) lead to the same volumetric sphere ratio”, i.e., and thus to the same particle mass ratios! Click ‘case AA for the Pion’, and case BB for the Kaon’ -- for such examples.
((Optionally, note the following, for that case presented much earlier in this this article, the 'Proton case BBB-CCC': That sketch shows the 'icosidodecahedron' positioning of 30 small spheres surrounding 1 sphere. It employs faces associated with icosahedron's triangles and dodecahedron's pentagons. (The 'icosahedron' and dodecahedron' are two platonic solid 'duals'.) That sketch, (30 small spheres surrounding 1 large sphere), was also found on an old plaque in an old Japanese Shrine, and was there before 'protons', etc., were even 'dreamed of'. And those plaques are described in a recent book, Sacred Mathematics: Japanese Temple Geometry, by F. Hidetoshi, T. Rothman. Similarly, regarding some other old plaques in that book, and some other particle-related sketches in my articles.))
Optional: For an Overview of the subject; one may also click “TABLE III - Visual Aids for other relationships”.
Optional: For further presentation of pattern relationships; one may optionally click “TABLE IV – Different sphere patterns, but giving the same volume”.
Optional: Some readers might find interesting how “sometimes, Symmetries provide math shortcuts”.
Let us start by commenting on the first table presented in this article, instead of the last three mentioned. (Some discourse, below, might already be obvious to the some who viewed my drawings, and such readers can skip some of the paragraphs below.)
In some simple geometric patterns (such as when three large touching spheres surround one or three small touching spheres) -- certain volumetric ratios arise. When comparing the masses of certain important particles (Pions, Kaons, and Protons – compared to electrons) certain particle mass ratios are also noted. That first table correlated the cases where the geometric volume ratios and average mass ratios were nearly equal – and features basic patterns where spheres are always outside one another.
The second (addendum) Table shows an additional case where the geometric volume ratios and average particle mass ratios are nearly equal, i.e., the Muon to Proton case. The second table is somewhat like the first; except in the second table, the sphere patterns are entirely inside of the larger spheres, and one of those enclosed set of spheres consists of only two spheres. (In fact, I would liked to have shown, correspondingly, only two large spheres outside of, and surrounding, one small sphere -- but for that, of course, the two large spheres would have never quite ‘gotten the horse corral closed’. Nor would that result in firm structures having ideal symmetry, simple combinatorics, or good basic structure.)
Had the large sphere we used - to calculate the Muon’s mass - been based on the Neutron (with mass equivalent to1838.68 electrons) instead of the Proton (1836.15 electron masses); our Muon mass estimate would have been still better; although landing slightly on the ‘high side’.
Our estimate does not “hit the exact center of the bull’s eye”, but is remarkably close. And let us remember this: The geometric patterns, used in all the above comparisons, are rather similar, and so very basic! And they had been previously used to make impressive estimates, in the first table, before attempting another satisfactory use of them. And, indeed, by using related patterns again -- other good comparisons were achieved! (I.e., see second table and the ‘List of major Hyperon Particles’.) And additional clickable links were provided allowing us to view other major patterns, i.e., different geometric roads but often giving the same ratio outcomes. Thus, I think that all the above, taken together, provides continuing connective and escalating evidence that the major relationships above are not likely coincidence!
Let us note and stress that the centers of all the spheres are co-planar in the patterns shown in Tables I & II above; and also in Table III, to be discussed further below.
Note, in the first table; the four-sphere pattern in case ‘A’ (the Pion case) -- would exactly fit into each of the three very large spheres shown in case ‘C’. (Case ‘C’ is the larger of the two co-acting patterns shown in case ‘B & C’ -- that generate our proton. There we show that an average sphere volume, calculated by considering the two co-acting patterns averaged together, represent our Proton The full geometric extension of the co-acting pattern shown in case ‘C’ extends beyond only the small portion of it shown in the first table.)
Optional: Now, a brief word about TABLE III – ‘Visual Aids for other relationships’. (See above Table III reference for a link to display it again, if necessary.) Remember the great extension of that co-acting pattern shown. It contains three very large spheres, any one of which could act as one ‘co-acting’ sphere. By comparison, the proton sphere is relatively small. The fraction by which the co-acting pattern in case ‘C’ (the ‘9-Pion’ pattern) exceeds the relatively modest proton’s radius – roughly represents the extra extension of ‘nuclear forces’ beyond a Proton’s (or a nucleon’s) surface. (Yukawa also used his own conception of ‘pion action’ to account for the extended range of nuclear forces.) All this paragraph may also relate to the magnetic field of the proton being several times greater ‘than expected’.
((Important: We described ‘an averaging of two spheres’, i.e., ‘co-acting’ spheres, as creating the Proton; but perhaps we could have alternately said that the pair of spheres were ‘co-factors’ in creating the Proton -- to borrow a chemist’s term! Or maybe even borrowed the term, ‘resonance-structure’ of spheres, the old term used by some chemists when describing the resulting length or strength of bond between carbon atoms of a benzene molecule when not purely a ‘double’ nor ‘single’ bond, but a sort of ‘average’ between the two.))
The reader is reminded of the above link to ‘Table IV – Different sphere patterns, but giving the same volume’. That illustrates how even some basic tetrahedral patterns of spheres (with non-coplanar centers) still generate the same volumes as simple ‘planar’ patterns do!
Any readers who find the above Tables I & II rather self-explanatory, may just quickly ‘scan’-over the four paragraphs below, or just skip them and scroll or click down to the next addendum.
_________________________________________________
The first two patterns, i.e., see first Table, case ‘A’ and case ‘B’, consist of three large spheres, in a triangular pattern, surrounding one and three small spheres, respectively. The volumetric ratios (large sphere to small sphere) are compared to the mass ratios of so-called ‘semistable’ mesons to electrons. (The ‘semistable mesons’ above are generally more stable than the vast number of particles that have been discovered since 1950. By today, so many different particles have been discovered, that many scientists consider ‘all the species’ as comprising ‘a particle Zoo!’ This article addresses the more basic ones: Case ‘A’ compares ‘Pions’ to electrons, and case ‘B’ compares ‘Kaons’ to electrons, and etc.
The last ‘pair’ of patterns shown in the first Table, cases ‘B’ & ‘C ‘, involves six equal small spheres. It also involves three ‘intermediate’ size spheres (as in case ‘B’), and three ‘larger’ spheres (shown in case ‘C’). The packing, in case ‘C’, is less efficient than case ‘B’, as each large sphere is touching only one small sphere instead of two. The average volumetric ratio (last pair of patterns) is the three ‘large’ spheres plus the three ‘intermediate’ size spheres divided by six small spheres. This volumetric ratio is compared to a mass ratio consisting of the average mass of a proton, antiproton, neutron and antineutron, to the mass of an electron. ((If the neutron and antineutron were ignored, the ratios comparison would be in better agreement. The proton is a stable particle, but the mean life of a neutron outside of a nucleus is about 12 minutes.))
Table II features the Muon, an important non-stable particle discovered in 1936. But it has a longer half-life than most particles discovered later. The corresponding geometric patterns shown might seem to “turn the first table’s paradigm ‘inside out’.” In fact, for quite a number of reasons, the Muon, historically, did turn the expectations of the middle 20th century physicists ‘inside out’! I.e., the muon did not turn out to be the (Pion) particle that Yukawa predicted – the Muon did not even turn out to be a ‘true meson’ at all! And when the muon’s unusual characteristics came to Rabi’s attention, Rabi reportedly exclaimed, “Who ordered that!” (the Muon).
From data in various books,1-4 or perhaps more recent sources, one may calculate or ‘check out’ the approximate ratios found in the first Table. ‘Wikipedia’ might be used as a preliminary source for the Muon and most other particles in the ‘particle Zoo’; but even better, it may refer readers to more the specialized (original) sources.
(In the above Tables, R and r denote the radii of large and small spheres, respectively.) ((The volumetric ratio (large sphere to small sphere) varies as the cube of their radii, i.e. (R/r)3.)) Of course, when we say, ‘this big sphere has 8 times the volume of this smaller sphere’, and ‘thus the big one represents an ethereal sphere with 8 times the mass of the smaller ethereal sphere; we assume that a uniform density of material or aether composes them. That is somewhat akin to the ‘Bohr liquid drop nucleus concept’ – that we describe later.
REFERENCES AND NOTES (OPTIONAL)
(1) Dalitz, R. H.; Goebel, C. In McGraw-Hill Encyclopedia of Science & Technology, 7th ed.; McGraw-Hill, Inc.: New York and other cities, 1992; Vol.10, "Meson". P 662
(2) Handbook of Chemistry and Physics, 73rd ed.; CRC Press: Boca Raton, FL, 1992; Section 1-2, Table 2, The 1986 Recommended Values of the Fundamental Physical Constants".
(3) Semat, H. Introduction to Atomic and Nuclear Physics, 4th ed.; Holt, Rinehart & Winston: New York, 1962; Chapter 15, p526.
(4) Note, for the more simple cases above: (3 spheres surrounding one; or 2 spheres inside of a large one; or 3 spheres inside of a large one) – those are also addressable using Descartes' Circle Theorem. That theorem is described in detail in Wikipedia using “Descartes’ theorem” in Wikipedia’s search window. It is applicable for calculating the unknown radius of a circle if the other circle radii are known – in cases where each circle touches all the others (i.e. is tangent to all the others), and provided all circles are in the same plane. (And it works, even in more complicated cases than our ‘pion’ and ‘muon’ cases; that is – even when the known radii are not of the same radius.
(5) Note, for more complicated cases, where the mutually touching spheres are non-planar: (4 medium-size spheres tetrahedrally directed and surrounding one small sphere; or those 4 spheres themselves surrounded by one larger sphere) – the so-called ‘Soddy-Gosset’ theorem may be used. Its form is somewhat like Descartes’ theorem, but slightly different; and it is also described in detail in the same Wikipedia article as addresses the ‘Descartes theorem’. And that Wikipedia article treats the subject even beyond all the above. (But, of course ‘good old trigonometry’ can also be used, instead, to address all my patterns in my article; and, in fact, must be used in cases where any one sphere does not touch every one of the others, i.e., cases where Descartes’ and Soddy-Gosset’s theorems don’t apply!)
(6) Note, it can be shown that each of the large spheres shown in case ‘C’ would just exactly enclose the 3-sphere triangular array of spheres shown in case ‘A’. And, incidentally, the volume of any very large sphere in case ‘C’ is exactly equal to the volume of the very small sphere at the center as shown in case ‘A’ plus 10 times the volume of any modest-sized sphere also shown in case ‘A’. (Of course, that assumes, as intended, that each of the very small spheres shown in cases ‘A’, ‘B’, and ‘C’ are equal.) Note #(6) can be most easily seen as true when the volume of each very small sphere is set equal ‘1 unit’ (a simple integer); and, incidentally, then the volume of each surrounding sphere in Cases ‘A’, ‘B’, and ‘C’ comes out as a ‘irrational’ number.
(7) The ‘case AA for the pion’, above, did not occur to me until 2011. Therefore, links for it, (and for cases ‘BB’ and ‘BB-CC’ in order to supplement and highlight aspects of older drawings) – were not added to my article until late 2011.
(8) Note, the possibility that aether consists of material spheres -- is mentioned in: Christian Huygens’s Treatise on Light (1678), English rendering by S. P. Thompson, 1912, University of Chicago Press, (Project Gutenberg eBook, book #14725, released 1-18-2005) http://www.gutenberg.org/etext/14725 Also note that Osborn Reynolds (of ‘Reynolds-Number’ fame) strongly advocated that ‘all space was filled with spheres’ in his book, The Sub-Mechanics of the Universe, Pub. for the Royal Soc. of London, Cambridge University Press, 1903.
(9) I thank Greg Volk for providing me his collection of calculations, pictures, and ‘Mathematica files’, Apr. 2008 and Nov., 2009, especially those addressing the more the complicated of sphere patterns relating to the more complicated ‘Platonic’ patterns. These were needed by me to address most Hyperons and related issues, since the Hyperons are also more complicated than the lighter, more conspicuous particles, generally discovered earlier. ______________________________________
Addendum (9-2-2007): Speculative Thoughts and Miscellaneous Comments
We now attempt to explain in more detail why particle mass ratios and geometric volume ratios are nearly equal, as described in this article. I doubt if it is just coincidental.
Historically, Huygen visualized a space filled with ethereal spheres for his effective treatment of light’s behavior. And even more so, Osborn Reynolds was convinced that spheres filled space! (I doubt that well defined, small spherical electrons actually dwell neatly between the large spherical nucleons in the nucleus, itself.) But I think that small and large ethereal spheres do likely exist in ethereal space! (Or something equivalent.) And that the large energized ethereal spheres have larger energies than the smaller ethereal spheres between them, and in proportion to their greater size. And they ‘communicate’ their different amounts of energy, respectively, to globs of dense matter that are ‘candidates’ to become particles, and thus help to create and stabilize particles of high and low energy, respectively, and high and low corresponding mass, respectively. I believe the following occurs, (or something like it):
Digest: There exists in most of space, spinning vortices (or the like) of ultra low density matter, rotating at ultra high speed. Perhaps they are spherical spinning balls of aether, (about the size of ‘the Bohr hydrogen atom’). These ultra high energy spinning ethereal balls help provide the ultra high ethereal pressure in space. Those ethereal balls have great spin -- roughly a Planck’s constant amount of angular momentum, despite their low density. That causes prospective long-life particles (like the proton) to develop roughly a Planck’s constant worth of angular momentum. Gross particles, such as the proton, must exhibit that much angular momentum to be compatible to the ethereal spinning spheres nearby, and thus survive. (Particle spin may also aid stability.)
Nuclear matter has approximately the highest density that compact matter can have in the universe. Protons (and electrons in the nucleus) are made of nuclear matter; and, therefore, they have very high density. (That concept is consistent with the Bohr ‘liquid drop model of the nucleus’.) The interaction, between the low density, ultra high pressure aether and the very high density nuclear matter, leads to, roughly, ‘the velocity of light’ as being the maximum speed that nuclear matter can obtain.
So the prospective stable proton is encouraged to form with these attributes: It has, roughly, the highest density of matter possible -- but, roughly, also exhibiting a ‘Planck’s constant’ worth of angular momentum as it spins. And it spins at roughly, ‘C’, the highest speed possible for high density bodies. And, physically, the proton maintains a nearly minimum spreading-out of itself through space (a great compactness) -- while still exhibiting that much angular momentum.
There exists in space -- small balls and very small balls of energized aether. These tend to form in patterns, as pictured previously; and therefore such ethereal balls are more stable than otherwise! The small and very small balls fit between the crevices of larger ball arrays, etc. Small balls of aether interact with the prospective proton. Some of those aether balls are somewhat larger and some are somewhat smaller, in size and energy, -- compared with the proton. But the average energy of those aether balls (i.e., some likely bigger and some likely smaller than the proton) roughly equals the energy of the proton. So an averaging, a sort of ‘equipartition’ of energy interaction occurs, and the proton helps promote that.
Thus, the spinning proton also causes much of space to form patterns consisting of small and very small sized ethereal spheres. Thus, these ethereal spheres contain small and very small quanta’s of energy, respectively. Those are illustrated in the pattern shown above, see first table. Then, those ethereal ball arrays, in turn, help to maintain the stability of the proton (by ‘feedback’), and the stability of the electron (a particle much less massive than the proton). And also some stability of some other important particles in physics!
Thus, the small and very small energies of the small and very small aether balls, respectively, help stabilize protons, electrons and other particles too. ((The rather non-concentrated electron, has to spread out, (perhaps like a spinning doughnut) to roughly generate a Planck’s worth of angular momentum. Thus it would seem, at first, that the electron would be a poor candidate for stability. But the many standard very small ethereal balls in space, that fit so well into the ethereal patterns in space, maintain the electrons’ stability, by sharing an equipartition of energy condition with it.
Optional: Incidentally, according to many theories; the ‘free’ electron is larger when it is outside the nucleus, i.e., it spreads out. And some detailed theories suppose that the free electron assumes a ‘doughnut-shape’ and that it is also like a twisted-dough doughnut. I.e., that is, it also rolls as it spins, (with say, a ‘clockwise’ roll if it is an electron, and ‘counter-clockwise’ roll if it is a ‘positron’, the mirror image of the electron). I have sometimes wondered if one layer of that ‘dough’ might be spinning, and a separate layer of ‘dough’ is rolling.
Some people have suggested that the electron structure is like one strand of a closed loop of rope, and one other strand is ‘rolled’, say, clockwise around it, and also completing a closed loop. But, if that other strand rolls ‘counter-clockwise’ instead of clockwise, it forms a ‘positron’ instead of an electron. (Perhaps, even a ‘stunt’ is being done mainly by an aether current around the electron instead of the electron’s material actions, itself. Or, perhaps, as well as the electron’s material, itself.))
Optional concluding remarks: An equilateral triangle has been depicted, by the mathematician, Richard Courant, as exemplifying the simplest figure in two-dimensions from a structural or ‘combinatorial’ point of view. And some ancient Greeks regarded a sphere as the perfect form. Those are like many of the patterns shown in my illustrations, above.
It is interesting to note that the non-spinning, non-charged (neutral) kaon particle tends to break up shortly into smaller particles that do spin! And those particles ‘develop’ so-called ‘charge’. And many of those, in turn, break up to form electrons, i.e., very stable elementary particles, with spin and so-called ‘charge’. Consider this: It seems very unlikely that the little mundane (non-spinning) type of kaon has a ‘standby’ miniature centrifuge inside it. Nor something like an automated sugar coating dip-bath to ‘surface coat’ the evolving elementary particles with ‘charge’ (like ‘M & M’ candy’s hard surface coatings)!
We, thus, conclude this: It is the appreciable spin of the major spinning ethereal balls (in space) that causes non-spinning particles in our world to develop spin! (Or break up into other particles that develop spin.) Those various style spins of various types of particles continue to spin in that environment. That spin and spinning environment is the cause of particles ‘attracting or repelling’ one another. That is what humans have chosen to call ‘electrostatics’. I.e., or Coulomb’s attraction and repulsion. In other words, to cope efficiently with the ensuing ‘paradigm’; humans have concocted the abstract word, ‘charge’, namely ‘positive charges and negative charges’! But ultimately, so-called ‘charge’ and charge behaviors are caused by Planck’s constant related spins of ethereal balls or vortices in space! And/or, perhaps there may also be corresponding ethereal (current-like) flows in loop patterns, in space, that also may contribute to stability, and the phenomena of electrostatics and electromagnetism.
If the reader wishes, he/she may click over to my article, ‘What We See and What We Don't See’, for estimates of the density, velocities and pressures of the ‘aether’ in space. One also finds there -- a somewhat speculative basic discussion of ‘combinatorics’, regarding the ‘primary attributes’ that ‘happen’ to be in this world, including ‘angular momentum per volume’.
______________________________________________
Optional, continued: To understand the great differences in magnitude manifested by electrical forces vs. nuclear forces vs. gravitational forces - I add these few pages of conjectures (to put all that in perspective):
In the case of the very strong ‘nuclear forces’; those strong forces arise because of the following factors: ‘Bernoulli-related’ forces arise, associated with the flow of very high density nuclear matter. That high-density flow arises within the nucleus and stays close to the nucleus, itself; and the flow is roughly at the speed of light. That, and the ‘Bernoulli equation’ (or principle), and the ultra-high external aether pressure -- causes the strong nuclear forces to develop, i.e., the strong so-called ‘attractive’ forces – with their short distance limitation.
In the case of electrical forces; electrical forces are also strong forces, but not as strong as nuclear forces. That is likely because the electric forces arise due do lower mass particles (or only part of more massive particles). Let us compare the forces required, say, to pull a proton apart compared to pulling a ‘nuclear electron’ away from a neutron. Here is an analogy: Von Guericke’s many horses could not pull his two large hollow ‘Magdelburg’ hemispheres apart (i.e., the proton case), but the horses could have easily pulled a small cork off a large bottle, having a similar vacuum interior (i.e., somewhat like pulling a small mass electron from a neutron – in our analogy).
Particles, such as the ‘free’ electron, (despite their often ‘puffed-up’ volumes) are not as able to fully harness the pressures of space, to create as much total force resultant -- compared to what the compact higher-mass particles accomplish. But the high ethereal pressures that those ‘free electric’ particles harness (especially when separated by quite some distance from other ‘charged’ particles) are due to much faster-than-light circulations of ‘thin aether’, subtly directed. (Some more details are provided in my other articles.)
Now for Gravitational forces: They are very weak forces compared to the nuclear and electrical forces, because they likely arise between two or more particles due to very weak ‘Bernoulli flow’ effects. Let me try to explain it better than I once did.
First and foremost, gravitational ‘attraction’ occurs, say, between two particles, because of an aether flow between them. And that aether flowing is a very low-density flow. And let us now compare that low density flow to the high-density flow of nuclear fluid, say, between two nuclei that are rather close together, i.e., ‘nuclear forces’. We first consider the cases where the aether and the nuclear fluid are flowing at the same velocity, which I think is close to reality regarding one aspect of aether flow: (The density of the flowing material is a major factor in Bernoulli’s equation that determines the forces arising.) Thus, when the velocity of the flows are equal, the gravitational forces will be lower by a magnitude proportional to the aether’s lesser density compared to thicker flowing nuclear fluid’s higher density. (Using a partial analogy, if you are hit by a 10 mph thin air breeze, you will be affected much less than if hit by a thick10 mph water stream!)
Of course, gravitational forces, although weak, can exert themselves at much greater distances than nuclear forces, because although the thick nuclear fluid flow is confined to close to the nuclei, the ethereal movements can extend out to very great distances through space! Of course, an ethereal ‘stream’ is less congested by two particles when the particles are widely separated – a factor causing the gravitational forces to be less when the two particles are very far apart. (And the ‘asymmetry’ in space is less, in the latter case, also.)
A final subtle point I wish to make is this: A quickly changing breeze can hit you at 10 mph in the face and then 10 mph in the back. But that does not mean that air molecules vibrate with only 10 mph speed, nor that the ‘speed of sound’ is only 10 mph. Instead, those underlying vibrations and speed are grossly greater -- closer to 800 mph.
Important: By analogy, I think that the aether in space is like a quickly changing cyclic air breeze; it has two vastly different velocities or movements associated with it. One is like the very fast (air) molecular or particle vibrations – the underlining speed. And the other is like the changing cyclic winds, say averaging a slow 10 mph, north to south and back again, say, in a second – the ‘over-lining’ speed. (Or, as in ‘radio broadcasting’, like a continuous very fast vibrating radio wave that can also be slowly modulated by the broadcaster’s voice.)
Like continually stirred-up windy little storms; we can imagine aether’s normal ‘little’ storms have a minimum current of about velocity ‘C’, the speed of light. But when, say, two neutrons are near one-another, they constrict the storm breezes (flowing or undulating between them). And, thus, the speed of flow increases slightly, say, to a speed slightly greater than ‘C’ between them. And, thus, a weak (Bernoulli-equation) related gravitational ‘attraction’ occurs. But the underlining ethereal super-fast vibrations or rotations are like our air molecular vibrations’ analogy. (not just storm breezes).. It consists of miniature ‘cells’ or a substructure vibrating or rotating at velocities far greater than ‘C’ by many magnitudes!
Gravitational action and sensitivity relates to the case of relatively slow ethereal cyclic drift, although superimposed on a much faster underlying ethereal vibration or rotation!
And I am not the first to say that sort of thing, nor have I likely said it better than some others. Yet, with all the above mentioned; I do not claim I know all the details regarding the interactions between the aether in space and gross matter -- regarding gravity, etc.
Back to: Home
Carl R. Littmann
(Readers’ comments
always welcome)